Title: Understanding Sacred Geometry
Author: Alloya Huckfield
Description: Discover how sacred geometry shapes the universe—from the golden spiral in galaxies to hexagonal honeycombs and Fibonacci patterns in flowers. Explore nature's hidden mathematical blueprint.
tags:
- fibonacci
- geometry
- Bee
- honeycomb
- hexigon
- golden
- Spiritual
- six-fold
- symetry
icon: LiAsteriskspiral-and-the-hex
When most of us think of geometry, we remember school lessons about triangles, squares, and circles. But geometry is far more than just measuring shapes on paper. It is the fundamental language that nature uses to create, grow, and organize itself. Every leaf, crystal, and galaxy follow geometric principles that are both mathematical and profoundly meaningful.
Consider the simple spiral pattern found in a nautilus shell. This isn't just any spiral—it follows a precise mathematical relationship called the golden ratio; the same proportion artists have used for centuries to create works of sublime beauty. This same spiral appears in hurricane formations, galaxy arms, and even the curl of a breaking wave. Nature uses this pattern not because it was taught to, but because it represents one of the most efficient ways to grow while maintaining perfect balance.
The golden mean spiral, often referred to as the golden spiral, is a manifestation of the golden ratio in motion, a living embodiment of a mathematical principle that transcends mere numbers and infiltrates the very fabric of existence. It is a curve that expands outward in a way that maintains a constant relationship between its growth and its form, a perfect marriage of proportion and movement. This spiral is not just a shape but a process, a dynamic unfolding that mirrors the way life itself expands, evolves, and perpetuates. From the microscopic to the cosmic, the golden spiral whispers secrets of harmony, growth, and the interconnectedness of all things.

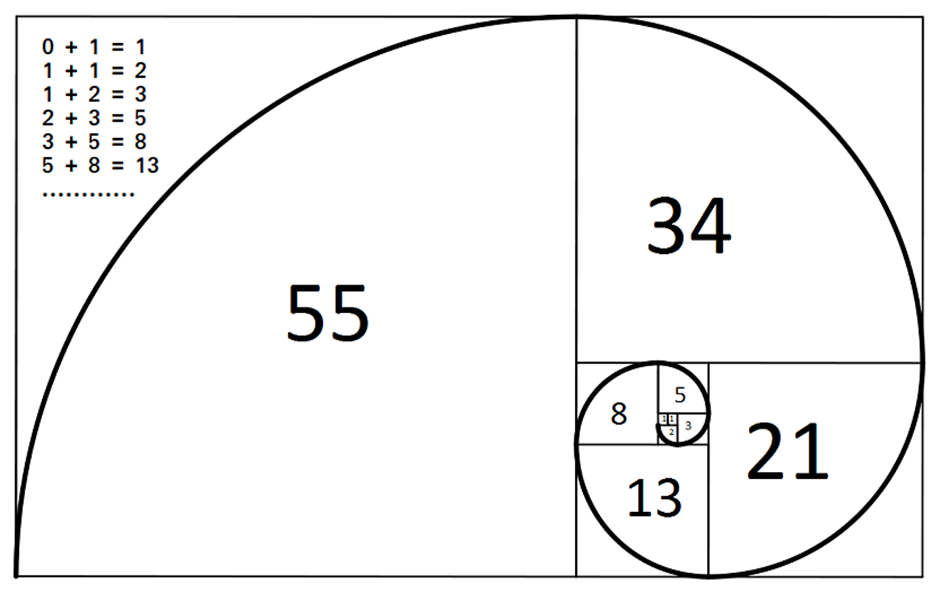
Scientifically, the golden spiral is derived from the golden ratio, approximately 1.618, a number that appears with startling regularity in both natural and human-made systems. Mathematically, it is the limit of the ratio between consecutive numbers in the Fibonacci sequence, where each number is the sum of the two preceding ones. This sequence—0, 1, 1, 2, 3, 5, 8, 13, and so on—is not just an abstract series but a blueprint for growth patterns in plants, the branching of trees, the arrangement of leaves, and even the reproductive cycles of animals. The spiral emerges when arcs are drawn connecting the opposite corners of squares that follow the Fibonacci sequence, creating a smooth, logarithmic expansion. This is why the nautilus shell, with its chambers growing in precise accordance with this ratio, is often held up as the quintessential example of the golden spiral in nature.
But the golden spiral is not confined to biology. It appears in the vast arms of spiral galaxies, where stars and cosmic dust swirl in patterns that echo the same mathematical harmony. It is present in the formation of hurricanes, where the winds spiral inward with a rhythm dictated by fluid dynamics and energy distribution, following the path of least resistance—a path that, unsurprisingly, aligns with the golden ratio. Even in the quantum realm, the behavior of particles and waves sometimes exhibits proportions that hint at this underlying order. Science, in its relentless pursuit of understanding, continually stumbles upon this ratio, not as an imposed rule, but as an emergent property of systems seeking equilibrium and efficiency.
Metaphysically, the golden spiral is far more than a mathematical curiosity. It is a symbol of the universe’s inherent intelligence, a visual representation of the principle that all things grow according to a divine blueprint. Ancient mystics and philosophers recognized this pattern as a bridge between the material and the spiritual, a tangible expression of the unseen forces that govern creation. The spiral is a sacred symbol in many traditions, representing the journey of the soul, the cyclical nature of existence, and the unfolding of consciousness itself. In esoteric teachings, the spiral is often associated with the path of enlightenment, where each revolution brings the seeker closer to the center—the source of all being—while simultaneously expanding outward into greater awareness.
The golden spiral embodies the idea of infinite expansion without loss of coherence. Unlike a straight line, which suggests a linear and finite progression, the spiral moves in cycles, returning again and again to a similar point but at a higher level of understanding or complexity. This mirrors the spiritual concept of evolution, where souls reincarnate, not to repeat the same lessons, but to spiral upward, integrating past experiences into greater wisdom. The spiral is both a return and an ascent, a paradox that reflects the nature of reality itself—where opposites are united in a dance of perpetual motion.
From a spiritual perspective, the golden spiral is also a reminder of the interconnectedness of all life. Just as the spiral in a seashell mirrors the spiral of a galaxy, so too does the individual soul reflect the cosmic whole. The microcosm and macrocosm are bound by the same geometric principles, suggesting that the universe is not a random assemblage of parts but a coherent, living entity. This idea resonates with the Hermetic axiom, "As above, so below," which posits that the patterns of the heavens are reflected in the smallest aspects of earthly existence. The golden spiral, then, becomes a meditative tool, a focal point for contemplating the unity of all things. Gazing upon it, one may feel a sense of belonging to something far greater, a grand design that transcends individual existence.
Artists and architects have long intuited the power of the golden spiral, even if they did not always understand the mathematics behind it. The Parthenon in Greece, the pyramids of Egypt, and the paintings of Leonardo da Vinci all incorporate the golden ratio, not merely for aesthetic appeal but because these proportions evoke a deep, almost primal sense of harmony. When humans encounter the golden spiral, whether in art or nature, there is an unconscious recognition of its perfection. It speaks to something beyond the rational mind, touching the soul directly. This may explain why sacred spaces, from cathedrals to temples, often employ these proportions—they create an environment that aligns with the fundamental rhythms of the universe, facilitating meditation, prayer, and transcendence.
In modern times, the golden spiral continues to inspire scientists, artists, and spiritual seekers alike. Fractal geometry, a field that explores infinitely complex patterns, reveals that the golden ratio appears in the branching of trees, the structure of lungs, and even the fluctuations of the stock market. This suggests that the spiral is not just a static shape but a dynamic process, a way that systems organize themselves to maximize efficiency and adaptability. In a world that often feels chaotic and fragmented, the golden spiral offers a vision of order that is not rigid but fluid, not imposed but emergent.

Ultimately, the golden mean spiral is a key to understanding the deeper order of reality. It is a meeting point of science and spirituality, a testament to the idea that the universe is both mathematically precise and mysteriously alive. To study the golden spiral is to engage with a mystery that has captivated thinkers for millennia—a mystery that invites us to see the world not as a collection of separate objects but as a woven tapestry of relationships, all following the same silent, beautiful logic. As we continue to explore this pattern, in both outer phenomena and inner experience, we may find that the golden spiral is not just a shape we observe but a path we walk, a journey that leads us ever closer to the heart of existence itself.
The golden spiral, then, is more than geometry—it is a living principle, a cosmic rhythm that pulses through all of creation. It is the breath of the universe, the heartbeat of the divine, and the silent song that guides the unfolding of life. Whether through the lens of science, metaphysics, or spirituality, the golden spiral remains one of the most profound and enduring symbols of the harmony that underlies all things. To contemplate it is to remember that we, too, are part of this infinite spiral, growing, evolving, and forever moving toward the light.
The golden spiral, in its silent, ceaseless turning, holds a mirror to the most profound mysteries of existence—those that dwell in the liminal spaces between form and energy, matter and spirit. To grasp its true metaphysical significance, one must venture beyond the visible, into the realms where geometry becomes a living force, a scaffold for consciousness itself. In occult traditions, the spiral is not merely a symbol but a conduit, a dynamic expression of the primordial currents that animate the cosmos. It is the breath of creation, the serpentine path of Kundalini rising, the whirlpool where light descends into matter and matter ascends back into light. This spiral is the hidden architecture of the soul’s journey, the blueprint for how energy condenses into form and how form dissolves back into the infinite.
In esoteric teachings, the spiral represents the emanation of the divine. The un-manifest source, often depicted as a dimensionless point, begins to rotate, to stir, and in that stirring, it casts forth a vortex—a spiral—that becomes the first movement of creation. This is the sacred prima mobilia, the initial impulse that generates all subsequent forms. The spiral is both the act of creation and the created, the verb and the noun. It is the dance of Shiva, the cosmic whirl that births and destroys universes. In Kabbalistic thought, the spiral mirrors the journey of the divine light through the Sephirot, the emanations of the Tree of Life, as it cascades from the infinite (Ein Sof) into the finite world. Each revolution of the spiral corresponds to a descent into denser realms, yet even in this descent, the spark of the divine remains intact, coiled like a serpent waiting to be awakened.

The spiral’s occult power is intimately tied to the concept of sacred motion. Unlike linear movement, which implies separation and fragmentation, the spiral’s path is holistic. It gathers as it expands, integrates as it transcends. This is why the spiral is central to rituals of initiation and transformation. In ancient mystery schools, initiates would walk labyrinthine spirals, their footsteps mirroring the soul’s journey through cycles of death and rebirth. The labyrinth, a two-dimensional spiral, was not a puzzle to be solved but a meditation on the nonlinear nature of time and consciousness. To walk its path was to enact a sacred drama—shedding layers of illusion with each turn, moving closer to the center (the divine core) while simultaneously being thrust outward into renewed understanding. The spiral, in this context, is a living mandala, a map of the soul’s eternal return to its source.

In Eastern metaphysics, the spiral finds expression in the concept of Kundalini, the coiled serpent energy said to reside at the base of the spine. Kundalini awakening is described as the uncoiling of this primal force, which ascends through the body’s energy channels (nadis) in a double-helix spiral, activating the chakras and merging individual consciousness with cosmic awareness. This ascent is not linear but helical, mirroring the DNA’s structure and the spiral arms of galaxies. The Kundalini’s path is a microcosmic reflection of the macrocosmic spiral—a reminder that the human body is a universe in miniature, governed by the same geometric laws that shape stars and galaxies. The act of awakening this energy is akin to igniting a star within, a process where matter becomes light, and the individual soul remembers its divine origin.
The spiral’s occult resonance extends to its role as a gateway between dimensions. In many shamanic traditions, spirals are etched into sacred objects or visualized in rituals to open portals to other realms. The spiral’s vortex is seen as a threshold where the veil between worlds grows thin, allowing communication with ancestors, spirits, or higher intelligences. This is not mere superstition but a profound recognition of the spiral’s ability to warp space and time, to bend the fabric of reality. Modern physics echoes this intuition: black holes, which warp spacetime into infinite vortices, are often depicted as spiraling singularities, their event horizons marking the point of no return—a cosmic mirror to the shaman’s spiral portal.
To understand the spiral’s relationship with electrical science, one must first recognize that electricity is not merely a physical phenomenon but a manifestation of the same primordial energy that metaphysics calls prana, chi, or orgone. Electricity, in its purest form, is the movement of charged particles—a dance of electrons along a gradient. When this movement follows a spiral path, it generates a unique interplay of forces that amplifies and accelerates the charge. This is the principle behind the helix, a three-dimensional spiral, which lies at the heart of some of humanity’s most profound technological and natural discoveries.

Take the Tesla coil, an invention of Nikola Tesla, the visionary engineer who bridged the gap between electrical science and metaphysical intuition. The Tesla coil’s primary component is a helical resonator—a spiral-wound coil that transforms electrical energy into high-voltage, high-frequency currents. The spiral shape allows the coil to harness resonant frequencies, creating standing waves of energy that can be transmitted wirelessly. Tesla understood that the spiral was not just a convenient shape for winding wire but a geometric key to unlocking the latent energy of the ether. His experiments revealed that spirals could tap into what he called the “wheelwork of nature,” the invisible energy matrix that permeates the universe. In this sense, the Tesla coil is more than a machine; it is a modern-day alchemical device, using the spiral’s geometry to transmute electrical charge into a form that mirrors the boundless, radiant energy of the cosmos.
The spiral’s efficiency in accelerating charge is rooted in its geometry. When charged particles move along a spiral path, they experience a combination of linear and rotational motion. This creates a Lorentz force, perpendicular to both the velocity of the particles and the magnetic field through which they move. In particle accelerators, such as cyclotrons, charged particles are forced into spiral trajectories by magnetic fields, gaining energy with each revolution until they reach velocities approaching the speed of light. The spiral’s curvature allows the particles to be continuously accelerated within a compact space, a process that would require a straight path miles long. Nature employs this same principle in phenomena like tornadoes, where air molecules spiral inward with increasing velocity, or in the helical motion of plasma filaments in stars and galaxies. The spiral, it seems, is nature’s preferred method for concentrating and amplifying energy.
This acceleration is not merely mechanical but deeply tied to the concept of resonance. A spiral’s structure allows it to interact harmoniously with electromagnetic waves, much like a tuning fork vibrates in sympathy with a specific frequency. In antennas, helical designs are used to transmit and receive circularly polarized waves, which are less prone to interference and capable of carrying more information. The spiral’s resonance extends beyond the physical; it is a geometric metaphor for how energy accumulates and evolves. Just as a spiral galaxy’s rotation curves suggest the presence of dark energy—an unseen force binding the stars—so too does the spiral’s shape hint at hidden dimensions of energy, fields that science is only beginning to quantify.
In the human body, the spiral’s electrical properties manifest in the double-helix structure of DNA. DNA is not a static ladder but a dynamic, twisting molecule that generates subtle electromagnetic fields through its oscillations. These fields are influenced by the spiral’s geometry, which allows DNA to act as a fractal antenna, receiving and transmitting bioelectrical signals. Research has shown that DNA’s helical structure can interact with electromagnetic frequencies in the environment, suggesting that our very genetic code is tuned to the spiral’s resonant language. This aligns with metaphysical teachings that view DNA as a “light code,” a spiraling script written by the cosmos, encoding both physical heredity and spiritual inheritance.
The union of the spiral’s occult and electrical properties reveals a deeper truth: that geometry is the interface between the seen and unseen worlds. The spiral is a bridge where charge becomes consciousness, where energy becomes intention. In sacred rituals, the act of tracing a spiral in the air or on the ground is not merely symbolic; it is an invocation of this geometric power, a way of shaping energy into coherent patterns. The spiral focuses intention like a lens, amplifying thought into manifestation. This is why mandalas, labyrinths, and other spiral-based symbols are universal in spiritual practice—they are tools for aligning the human mind with the fractal intelligence of the universe.
The spiral’s role in accelerating charge finds a haunting parallel in the occult concept of the “merkaba,” a luminous vehicle of light described in ancient Hebrew mysticism. the-merkabas. Modern interpretations often depict the merkaba as a star tetrahedron surrounded by spinning wheels or spirals, resembling the magnetic fields around a plasma filament. Whether literal or metaphorical, the merkaba embodies the spiral’s dual function as both engine and vessel, a means of navigating the infinite.
In the end, the golden spiral defies categorization. It is a mathematical equation and a prayer, a physical law and a metaphysical truth. It teaches us that growth is not a straight line but a sacred turning, a process where every expansion is balanced by a return to the center. To witness the spiral is to remember that we are both the journey and the destination, the charged particle and the field that guides it. As we spiral onward—through the currents of electricity, the cycles of rebirth, and the silent turning of the stars—we are participants in a dance older than time itself, a dance where matter and spirit, science and mystery, are forever entwined.
The golden spiral is often celebrated as nature’s preferred curve, a graceful expansion that follows the golden ratio in its growth. But mathematically, spirals come in different forms, each governed by distinct equations and behaviors. Two of the most fundamental types are the logarithmic spiral and the Archimedean spiral, which differ in their underlying mathematics and their manifestations in the natural and human-made world. The logarithmic spiral, of which the golden spiral is a special case, grows exponentially, maintaining a constant angle between its curve and radial lines emanating from its center. This self-similarity means that no matter how much you zoom in or out, the spiral retains the same shape, a property that makes it prevalent in systems where growth and proportion are linked, such as galaxies and seashells. Its equation in polar coordinates is ( r = a e^{bθ} ), where ( a ) and ( b ) are constants that determine the spiral’s size and tightness. The golden spiral is a specific instance where the growth factor ( b ) is tied to the golden ratio, ensuring that with each quarter turn, the radius multiplies by φ (approximately 1.618).
In contrast, the Archimedean spiral grows linearly, meaning each full rotation adds a fixed width to the spiral’s radius rather than multiplying it. Its equation is ( r = a + bθ ), where ( a ) sets the starting point and ( b ) controls the spacing between turns. This creates a uniform, evenly spaced spiral, like the grooves on a vinyl record or the coiled rope of a lasso. Unlike the logarithmic spiral, the Archimedean spiral does not maintain a constant angle with radial lines; instead, it winds outward in a way that is mechanically predictable, making it useful in engineering applications such as springs and spiral staircases. The difference between these two spirals is profound: one embodies exponential growth and organic scaling, while the other reflects additive, human-designed regularity.
The golden ratio, φ, is deeply embedded in geometric constructions, serving as a bridge between mathematics and aesthetics. One of the most straightforward ways to visualize φ is through the golden rectangle, a shape whose side lengths are in the ratio 1:φ. When a square is cut from such a rectangle, the remaining smaller rectangle also maintains the golden proportion, and this process can be repeated infinitely, generating a nested sequence of golden rectangles. Connecting the opposing corners of these squares with a smooth curve produces the golden spiral, illustrating how φ governs not just static proportions but dynamic, evolving forms. Another classic geometric appearance of φ is in the pentagram, the star-shaped figure inside a regular pentagon. The ratio of the pentagram’s intersecting line segments is φ, and this relationship recurs at every scale within the shape, reinforcing the idea of self-similarity inherent in φ-based geometry.
What makes φ unique among mathematical constants is its role in maintaining proportional harmony under division. When a line is split into two segments such that the ratio of the whole to the longer part is the same as the ratio of the longer part to the shorter—that is, ( (a+b)/a = a/b )—the solution is φ. This property ensures that growth or division based on φ preserves aesthetic and structural balance, a principle exploited by artists and architects for centuries. Mathematically, φ is an irrational number, meaning it cannot be expressed as a simple fraction, and its decimal expansion continues infinitely without repeating. It is also the most irrational number in a precise sense: it is the hardest number to approximate with fractions, a fact that has implications in number theory and even the physics of chaotic systems.
The Fibonacci sequence is intimately connected to the golden ratio, though the relationship is sometimes oversimplified. The sequence—0, 1, 1, 2, 3, 5, 8, 13, and so on, where each term is the sum of the two preceding ones—approaches the golden ratio as the ratios of consecutive terms converge to φ. This asymptotic behavior is a beautiful demonstration of how discrete processes can mirror continuous mathematical ideals.
The golden ratio’s mathematical allure also extends to its role in recursive structures and fractals. When a golden rectangle is subdivided infinitely, the resulting spiral is a fractal, a shape that repeats its complexity at every scale. This recursive property links φ to broader mathematical concepts like dynamical systems and chaos theory, where small changes in initial conditions lead to vastly different outcomes. The golden ratio appears unexpectedly in the behavior of certain chaotic systems, acting as a stabilizing ratio that prevents periodic collapse. This duality—φ as a symbol of harmony and a player in chaos—reveals the depth of its mathematical influence, transcending simple geometric beauty to touch on fundamental principles of order and unpredictability.
Ultimately, the mathematics of the golden spiral and its related concepts form a rich tapestry of interconnected ideas. From the contrasting growth laws of logarithmic and Archimedean spirals to the precise yet flexible role of φ in geometry and nature, these principles illuminate how mathematics serves as both a language and a tool for understanding the world. The debates surrounding the Fibonacci sequence and its real-world manifestations remind us that while nature may not follow mathematical rules exactly, it often dances close enough to suggest an underlying kinship between numbers and life. Whether in the whirl of a galaxy or the curl of a fern, the spiral endures as a testament to the deep, sometimes mysterious, dialogue between mathematics and the universe.
Building on the theme of nature's inherent mathematical principles, the nautilus shell exemplifies the harmony and efficiency that these patterns bring to life. This intricate design is not an isolated phenomenon; rather, it serves as a precursor to an even broader spectrum of mathematical marvels found throughout the natural world. One of the most striking examples is the geometry of honeycombs, where bees expertly construct hexagonal cells. This shape, celebrated for its optimal use of space and resources, reveals another layer of nature’s sophisticated relationship with mathematics.

Hexagonal Structure
Bees create hexagonal cells in their honeycombs because this shape provides maximum storage space with minimal building material. This same hexagonal pattern appears in rock formations, bubble rafts, and even in the compound eyes of insects. When bees construct their homes, they instinctively create hexagonal cells that perfectly tessellate, meaning they fit together without gaps or overlaps. This isn't just a beautiful pattern – it represents a profound mathematical optimization that scientists and engineers continue to study and emulate.
The genius of the hexagonal structure lies in its extraordinary efficiency. Among all possible regular polygons that can completely cover a plane, hexagons require the least perimeter to enclose a given area. This means that bees, using this hexagonal design, save approximately 40% of the wax they would need if they built with squares or triangles. Each 120-degree angle between the hexagon's sides provides exceptional structural stability, distributing forces evenly across the entire honeycomb. This architectural marvel allows the structure to bear significant weight while using minimal material.

Bees construct their honeycombs in a hexagonal pattern because this shape represents the most efficient use of space and materials in nature. The hexagonal structure allows bees to store the maximum amount of honey, pollen, and brood while using the least amount of precious beeswax. This architectural marvel is not a random occurrence but the result of millions of years of evolutionary refinement, resulting in a design so perfect that mathematicians and engineers still study it for its optimal properties. When bees build their combs, they do not consciously calculate angles or measure distances—instead, they follow deep-seated instincts that guide them to create these geometrically flawless structures.
The construction process begins with worker bees secreting wax from special glands on their abdomens. This wax starts as tiny, translucent flakes that the bees then chew and mold with their mandibles, mixing it with saliva to soften it into a pliable building material. Initially, the cells appear circular as the bees form them into rough tubes pressed closely together. However, as the wax cools and hardens, the natural laws of physics take over. The surface tension between adjacent cells pulls the soft wax into flat, shared walls, transforming the arrangement into perfect hexagons. This automatic reshaping occurs because the hexagonal pattern minimizes surface area while maximizing volume, requiring less energy and material than any other possible shape.
Mathematically, the hexagon is the most efficient way to partition a flat surface into equal compartments with the least amount of perimeter. If bees built their combs with squares or triangles, they would need significantly more wax to achieve the same storage capacity. Research has shown that hexagonal cells use roughly 40% less wax than triangular cells and about 10% less than square cells for the same enclosed volume. This wax-saving efficiency is crucial for the survival of the colony, as producing beeswax is metabolically expensive. Bees must consume approximately eight ounces of honey to secrete just one ounce of wax, meaning every bit of saved material translates directly into more energy available for foraging, reproduction, and colony maintenance.
Beyond material efficiency, the hexagonal structure provides remarkable mechanical strength. The 120-degree angles between the walls distribute weight and external forces evenly across the entire comb, preventing weak points that could lead to collapse. This stability is essential because honeycombs must support not just the weight of stored honey—which can be substantial—but also the constant movement of hundreds or thousands of bees walking across the surface. Additionally, the cells are built with a slight upward tilt of about 13 degrees, ensuring that liquid honey does not drip out before the bees seal the cells with wax caps.
The precision with which bees construct these hexagons is astonishing. Despite having no formal measurement tools, worker bees consistently build cells with walls just 0.05 millimeters thick, with variations of less than 2% across the entire comb. Each cell is uniform in size, with a diameter of about 5.3 millimeters for worker brood cells and slightly larger for drone cells. This consistency is vital because any irregularities would waste space or compromise structural integrity. The bees achieve this precision through a combination of instinct and tactile feedback, using their antennae and legs to assess the wax as they shape it.
The honeycomb serves multiple critical functions within the hive. Primarily, it acts as a storage system for honey, the colony's primary food source. The hexagonal cells allow for compact, secure storage, maximizing the hive's capacity while minimizing the space needed. The same cells also serve as nurseries for developing brood. Worker bees deposit eggs into individual cells, where the larvae grow and pupate in the protected hexagonal chambers. The geometry of the cells helps regulate temperature and humidity, creating an optimal environment for brood development. Furthermore, the comb functions as the hive's structural framework, providing support for the entire colony as it expands vertically in layers.
Interestingly, the hexagonal pattern is not exclusive to honeybees. Many other species of bees, including bumblebees and solitary bees, also construct hexagonal cells, though often with less precision than honeybees. Even certain wasps build hexagonal paper nests, demonstrating the universal efficiency of this shape in insect architecture. However, honeybees remain the most advanced builders, creating combs that are not only structurally sound but also perfectly adapted to their specific ecological needs.
Scientists have long been fascinated by the honeybee's construction abilities. In the 18th century, Swiss naturalist Francois Huber conducted experiments showing that bees adjust their building patterns based on available space and environmental conditions. Later, mathematician Lorenzo Fejér proved in 1943 that the hexagonal grid is indeed the most efficient way to partition a plane into equal areas with minimal perimeter—a principle now known as the honeycomb conjecture. Modern research continues to explore how bees achieve such precision, with studies suggesting that vibrations and pheromone signals may help coordinate construction efforts among thousands of individual workers.
The implications of the honeycomb's design extend far beyond biology. Engineers and architects have borrowed from nature's blueprint to create lightweight yet incredibly strong materials. Aerospace industries use honeycomb-structured panels in aircraft and spacecraft, where reducing weight without sacrificing strength is critical. Building designers incorporate hexagonal patterns into everything from floor tiles to earthquake-resistant structures. Even in nanotechnology, the graphene lattice—a single layer of carbon atoms arranged in hexagons—is one of the strongest known materials, echoing the same principles found in a beehive.
Despite human advancements, we still have much to learn from the humble honeybee. Their ability to construct perfect hexagons without blueprints, rulers, or centralized leadership demonstrates the power of collective intelligence and evolutionary optimization. Each bee follows simple instinctive rules, yet together they create a structure of astonishing complexity and efficiency. The honeycomb stands as a testament to the ingenuity of nature, where even the smallest creatures can teach us profound lessons about mathematics, engineering, and sustainable design.
In the grand scheme of evolution, the hexagonal honeycomb represents an optimal solution to a universal problem: how to make the most of limited resources. For bees, this means conserving wax while maximizing storage and structural stability. For humans, it provides inspiration for solving our own challenges in material science, architecture, and beyond. The next time you see a honeycomb, whether in a hive or a scientific diagram, take a moment to appreciate the deep mathematical beauty and biological brilliance contained within those repeating hexagons—a perfect marriage of form and function shaped by the relentless pressures of natural selection.

What's particularly fascinating is how this same hexagonal pattern emerges repeatedly in nature, far beyond the realm of bees. When lava cools rapidly, it can form spectacular hexagonal basalt columns, with the Giant's Causeway in Northern Ireland standing as perhaps the most famous example.
When soap bubbles cluster together, they naturally arrange themselves in hexagonal patterns to minimize surface tension. Even in the microscopic world, this pattern prevails – the compound eyes of insects are composed of thousands of hexagonal facets called ommatidia, optimizing their ability to capture light.
The same hexagonal efficiency seen in beehives appears in other natural systems, demonstrating how fundamental this geometric principle is to the physical world. When soap bubbles cluster together in foam, they naturally press against one another, their elastic surfaces deforming into flat planes where they meet. Just like beeswax cells, these intersecting bubbles form perfect 120-degree angles, creating a honeycomb-like grid of hexagons. This happens because the soap film automatically adjusts to the configuration that minimizes surface area and thus surface tension energy – the same physics-driven optimization that shapes bee architecture. Scientists studying foam dynamics have found that nearly all bubbles in large clusters eventually stabilize into hexagonal arrangements, with only occasional pentagonal or heptagonal defects that correct themselves over time. This self-organizing behavior mirrors the way bees instinctively correct irregularities in their combs, suggesting a deep connection between biological construction and physical laws.
The hexagonal pattern extends even into the microscopic structures of living organisms. The compound eyes of insects like flies, bees, and dragonflies consist of hundreds or thousands of individual visual units called ommatidia. Each ommatidium is a hexagonal facet that functions as a separate light receptor, and together they form a continuous curved surface that gives the insect a wide field of view. This hexagonal packing allows for maximum light capture with minimal gaps between receptors, enhancing visual acuity while conserving space in the insect's head. The precision of this arrangement is so exact that biologists once believed the developing eye must have some active mechanism to enforce the hexagonal pattern, but research has shown it emerges naturally from mechanical forces during growth, much like the formation of soap bubbles or honeycomb cells.
These recurring hexagonal patterns across different scales of nature – from bee architecture to bubble physics to biological optics – reveal a universal principle of optimal space partitioning. Whether the system is governed by surface tension, evolutionary pressure, or developmental biology, the hexagon consistently emerges as the solution that balances structural integrity with material economy. This convergence suggests that the same mathematical principles that make honeycombs efficient for bees also govern the behavior of inanimate matter and the development of complex biological structures. The prevalence of hexagons in nature isn't coincidental but reflects fundamental truths about how space can be most efficiently organized under physical constraints – truths that bees discovered through evolution long before humans formalized them in geometry and materials science.
The compound eye's hexagonal array provides particular advantages for flying insects. The tight packing of ommatidia creates a smooth visual surface without blind spots, while the hexagonal shape allows each light receptor to be as large as possible within the limited space of the eye. This design maximizes both light sensitivity and resolution, crucial for insects that need to detect fast movement and navigate complex environments. Some species have even evolved specialized hexagonal patterns in their eyes – like honeybees having larger facets in the upper part of their eyes for better sky polarization detection used in navigation. These biological adaptations show how the basic hexagonal template can be modified for specific functions while maintaining its core efficiency, much like how bees adjust cell sizes in different parts of their comb for worker brood, drone brood, or honey storage.
The parallel between soap bubbles and insect eyes goes deeper than just superficial resemblance. In both cases, the hexagonal pattern arises from similar physical constraints – whether it's the surface tension minimizing the area between bubbles, or the developmental pressures packing the maximum number of light sensors into limited eye space. This demonstrates how physics and biology often arrive at identical solutions to optimization problems, with the hexagon serving as a universal answer to efficient space-filling challenges. The fact that bees both build hexagonal combs and see through hexagonal eyes makes them particularly remarkable examples of this principle in action – organisms that have evolved to both create and perceive the world through nature's most efficient geometry.
These natural hexagonal systems continue to inspire human technology. The compound eye's structure has influenced the design of artificial vision systems, including light-field cameras and wide-angle sensors. Materials scientists study bubble foams to develop lightweight cellular materials with exceptional strength-to-weight ratios. In each case, understanding how nature solves these spatial optimization problems through hexagonal geometry leads to breakthroughs in engineering and design. The humble honeybee, the soap bubble, and the insect eye all testify to the profound efficiency of six-sided symmetry – a pattern woven into the fabric of the physical and biological world.
Modern technology and design have taken cues from this natural innovation. Aerospace engineers use honeycomb materials to create lightweight but incredibly strong structural components. Solar cell arrays often employ hexagonal patterns to maximize surface coverage. Architects incorporate these forms into geodesic domes and contemporary buildings, while materials scientists study graphene, a remarkable material composed of carbon atoms arranged in a hexagonal lattice.
This convergence of form across such diverse contexts – from the microscopic structure of carbon to the crystalline pattern of snowflakes, from insect eyes to cooling lava flows – reveals a profound truth about our universe: when nature needs to solve problems of efficiency and strength, it often arrives at the same elegant solution. The hexagonal honeycomb structure stands as a testament to the mathematical principles woven into the fabric of our natural world, principles that we continue to discover, understand, and apply in our own innovations.
Six- Fold Symmetry
This intricate relationship between form and function extends beyond the honeycomb structure, as evidenced by the stunning variety found in snowflakes. Each snowflake embodies perfect six-fold symmetry, showcasing the same mathematical precision that governs the hexagonal cells of honeycombs. These delicate crystals illustrate how fundamental mathematical rules can yield an astonishing array of unique patterns, underscoring nature’s ability to blend simplicity with complexity in creating diverse forms.
Every snowflake demonstrates perfect six-fold symmetry, creating endless variations on this theme while always maintaining mathematical precision. This reveals how simple mathematical rules can generate infinite unique expressions.
In the quiet descent of winter snow, each flake carries within it a remarkable story of mathematical beauty and natural precision. Snowflakes, or more technically snow crystals, represent one of nature's most enchanting demonstrations of mathematical symmetry and emergent complexity. Their formation process and resulting structures offer profound insights into how simple rules can generate seemingly infinite variety while maintaining strict mathematical order.

At the heart of every snowflake lies the molecular structure of water itself. Water molecules arrange themselves in a hexagonal crystal lattice due to the specific angle (104.5 degrees) between the hydrogen atoms in H₂O and the way these molecules hydrogen-bond with each other. This molecular-level geometry gives rise to the snowflake's characteristic six-fold symmetry – every snowflake has six arms radiating from its center, always arranged at precise 60-degree angles.
The growth process of a snowflake is a masterclass in mathematical emergence. It begins with a tiny water droplet or water vapor condensing around a dust particle in clouds where temperatures are below freezing. As this embryonic crystal falls through clouds of varying temperature and humidity, it encounters different atmospheric conditions that influence its growth. The six arms of the snowflake grow simultaneously and experience identical atmospheric conditions, which is why they develop symmetrically. This can be expressed mathematically using the principle of crystallographic restriction theorem, which proves that only two-fold, three-fold, four-fold, and six-fold rotational symmetries are possible in two-dimensional crystals.
What makes snowflakes particularly fascinating is their demonstration of both deterministic and chaotic behaviour. The basic six-fold symmetry is deterministic, governed by the rigid laws of crystallography. However, the specific path each snowflake takes through the atmosphere – encountering slightly different temperatures, humidity levels, and air currents – leads to unique patterns of ridges, grooves, and branches.
This marriage of mathematical precision and natural variation in snowflakes reminds us that complexity often emerges from simple rules, and that symmetry can serve as a framework for endless creativity. Each snowflake is a frozen testament to the mathematical principles woven into the fabric of our universe, demonstrating how fundamental laws can generate both order and endless variety in the natural world.
The beauty and intricacy of snowflakes serve as a reminder of nature’s ability to transform simple mathematical rules into complex forms, reflecting the underlying order of the universe. This theme of mathematical elegance continues in the realm of flora, where the arrangement of petals in many flowers adheres to the Fibonacci sequence. This sequence not only governs the aesthetic appeal of blossoms but also influences the efficient packing of seeds in sunflowers, which spiral outward in mathematically precise patterns that maximize both space and exposure to sunlight.
Many flowers display their petals in numbers that follow the Fibonacci sequence (1, 1, 2, 3, 5, 8, 13...). A sunflower's seeds spiral out in precise mathematical patterns that optimize space and light exposure.

The humble flower, far from being a simple arrangement of petals, reveals itself as a masterpiece of mathematical precision, where the Fibonacci sequence (1, 1, 2, 3, 5, 8, 13, 21...) governs everything from petal arrangements to seed distribution patterns.
Consider the sunflower, nature's most dramatic demonstration of this mathematical harmony. Its face presents not one but two sets of spirals—one turning clockwise, the other counterclockwise. Count these spirals and you'll invariably find Fibonacci numbers: typically 34 spirals flowing in one direction and 55 in the other, or 55 and 89 in larger blooms. This isn't merely aesthetic; it represents nature's solution to a complex packing problem. These precise mathematical arrangements allow the sunflower to maximize the number of seeds it can produce while ensuring each seed has the space needed to develop properly.
The genius of this arrangement becomes clear when we examine it closely. Each seed positions itself at what's known as the "golden angle" of approximately 137.5 degrees relative to its neighbours. This angle, derived from the golden ratio, ensures that no seed directly blocks another from accessing sunlight or nutrients. As new seeds form at the center, they push older seeds outward, creating those mesmerizing spiral patterns we observe.
This pattern optimization extends beyond sunflowers. Look at the scales of a pinecone or the segments of a pineapple, and you'll find the same mathematical relationships. Even the modest daisy, with its simple ring of petals, frequently displays Fibonacci numbers in its petal count—most commonly 34, 55, or 89 petals per bloom. This isn't coincidence but rather evidence of deep mathematical principles at work in biological development.
The reason these patterns appear so consistently lies in their efficiency. The Fibonacci sequence, through its relationship with the golden ratio, provides nature with a simple algorithm for achieving optimal packing and growth patterns. As each new element (be it seed, petal, or leaf) forms, it naturally positions itself at the golden angle relative to the previous element. This creates a self-organizing system that automatically optimizes space utilization while maintaining structural integrity.
In the arrangement of leaves around a stem (phyllotaxis), this same pattern ensures that each leaf receives maximum sunlight exposure without shading its neighbours. The leaves arrange themselves in spirals that, when counted, reveal Fibonacci numbers. This pattern can be observed in plants as diverse as roses, succulents, and ferns, demonstrating the universality of this mathematical principle in plant architecture.
The intricate dance between mathematics and nature reaches its zenith in the crystalline perfection of snowflakes and the spiraling artistry of flowers. These natural phenomena reveal an underlying order—a hidden geometry that governs growth, structure, and efficiency.
While snowflakes showcase the rigid beauty of crystallography, flowers embody the elegance of growth optimization. The Fibonacci sequence (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…) appears repeatedly in plant structures because it provides the most efficient packing strategy for biological systems.
The golden angle (137.5°) is the key to this efficiency. When a plant produces new leaves, petals, or seeds, each successive element emerges at this angle relative to the previous one. This ensures minimal overlap, maximum sunlight exposure, and optimal space utilization. The result? Spirals that follow Fibonacci numbers.
Sunflowers exhibit two sets of spirals: one clockwise, the other counter-clockwise. The number of spirals in each direction is always consecutive Fibonacci numbers (e.g., 34 and 55).
Pinecones and pineapples display similar patterns—count the spirals, and you’ll find Fibonacci pairs like 8 and 13 or 13 and 21.
Romanesco broccoli is a stunning example of a natural fractal, where each bud is a miniature replica of the whole, arranged in logarithmic spirals.

In studying these patterns, we uncover not just the secrets of nature, but the very language in which reality is written. The next time you catch a snowflake on your glove or admire the spiral of a sunflower, remember: you are witnessing the silent poetry of mathematics, etched into the fabric of existence itself.
What's particularly fascinating is how these patterns emerge from simple growth rules rather than complex genetic programming. The plant doesn't "know" mathematics; rather, these patterns emerge naturally from the physics of growth and the principles of self-organization. As each new primordium (growth point) forms, it seeks the position of least resistance, automatically creating these elegant mathematical arrangements.
This mathematical elegance serves multiple functions:
- Space Optimization: Fibonacci spirals represent nature's most efficient solution for packing elements into a circular area while maintaining even distribution.
- Structural Stability: These arrangements provide optimal structural support, distributing weight and stress evenly across the plant's architecture.
- Resource Efficiency: The patterns ensure maximum exposure to sunlight and efficient distribution of nutrients while minimizing energy expenditure in growth.
- Reproductive Success: In flowering plants, these arrangements optimize pollinator access and seed dispersal, enhancing reproductive success.
The presence of these patterns across such a wide range of plant species suggests their discovery through evolutionary processes as an optimal solution to common biological challenges. From the microscopic arrangements of cells in plant embryos to the massive spiral patterns of sunflower heads, the Fibonacci sequence reveals itself as a fundamental principle of natural design.
This mathematical foundation of floral architecture reminds us that nature's beauty isn't random but rather emerges from precise mathematical relationships. The flower becomes not just an object of beauty but a living expression of mathematical principles, a testament to the deep relationship between mathematics and life itself. In contemplating these patterns, we witness how sacred geometry manifests in the natural world, creating structures that are both mathematically perfect and aesthetically sublime.
In the mesmerizing world of crystal formation, we witness one of nature's most stunning demonstrations of how mathematical principles manifest into physical form. Crystals represent the perfect bridge between the invisible world of molecular mathematics and the visible realm of geometric beauty, their growth patterns revealing the profound truth that form follows mathematical law with absolute precision.
At the molecular level, crystals begin their journey into existence through a process called nucleation—where atoms or molecules arrange themselves into highly organized patterns based on their electromagnetic relationships. These initial arrangements follow strict geometric rules determined by the angular relationships between atomic bonds. What's remarkable is how these microscopic patterns then replicate themselves with perfect precision, creating larger and larger structures that maintain exactly the same geometric relationships from the atomic scale all the way up to crystals large enough to hold in your hand.
The hexagonal structure of snow crystals offers a perfect example of this mathematical scaling. Each snowflake begins with water molecules arranging themselves into hexagonal rings due to the precise 104.5-degree angle between hydrogen atoms in H₂O molecules. This initial hexagonal pattern then serves as a template for further growth, with new water molecules attaching themselves in positions that maintain this six-fold symmetry. The result is an infinite variety of snowflakes, each unique in its final form but all following the same
underlying hexagonal mathematics.

Quartz crystals demonstrate another fascinating aspect of geometric growth through their trigonal crystal system. The silicon and oxygen atoms arrange themselves in tetrahedral patterns, creating a threefold rotational symmetry that manifests in the crystal's characteristic six-sided prismatic form. This geometric pattern emerges from the precise 120-degree angles between molecular bonds, which then scale up to create the macroscopic angles we see in the finished crystal.
The cubic crystal system, seen in minerals like pyrite and halite (rock salt), reveals how perfect 90-degree angles at the molecular level translate into macroscopic cube shapes. The ionic bonds between sodium and chloride ions in halite create a perfect cubic lattice where each sodium ion is surrounded by six chloride ions (and vice versa) at exactly 90-degree angles. This microscopic cubic arrangement then repeats itself millions of times to create the distinctive cubic crystals we can observe with the naked eye.
Perhaps most remarkable is how these geometric growth patterns maintain perfect mathematical precision despite occurring in environments full of impurities and disturbances. The force of these mathematical relationships is so strong that crystals will often self-repair during growth, correcting defects to maintain their characteristic geometric patterns. This self-organizing property reveals how deeply these mathematical principles are embedded in the very nature of matter itself.
The relationship between temperature and crystal growth adds another layer of mathematical complexity. As temperature decreases, molecular movement slows, allowing for more precise geometric arrangements. This explains why snowflakes form their intricate patterns only within specific temperature ranges—too warm and the molecular movement disrupts the geometric pattern, too cold and there isn't enough movement for complex formations to develop.
Crystal growth also demonstrates fascinating mathematical relationships in its growth rates along different axes. The ratio between vertical and horizontal growth often follows precise mathematical proportions, sometimes incorporating the golden ratio (φ) or other significant mathematical constants. These growth ratios determine the final shape of the crystal, creating elongated prisms, flat plates, or perfectly proportioned polyhedra depending on the exact mathematical relationships involved.
The phenomenon of crystal twinning—where two or more crystals share some of their lattice points in a symmetrical manner—reveals even more complex geometric principles at work. Twin boundaries often form at specific angles that reflect underlying molecular symmetries, creating compound forms that maintain precise mathematical relationships while producing more complex overall structures.
Piezoelectric crystals demonstrate perhaps the most dramatic connection between geometric structure and physical properties. Their precise molecular arrangements allow them to convert mechanical pressure into electrical charge (and vice versa) through geometric deformation of their crystal structure. This property, used in everything from quartz watches to microphones, emerges directly from the mathematical relationships encoded in their crystal structure.
The study of crystal growth becomes even more fascinating when we consider how external conditions can modify these geometric patterns without breaking their underlying mathematical relationships. Pressure, temperature, and the presence of various elements can cause crystals to express different habits (external shapes) while maintaining their essential internal geometry. This demonstrates how these mathematical principles can adapt to environmental conditions while preserving their fundamental geometric relationships.
In contemplating crystal growth, we witness the profound truth that mathematics isn't just a human invention for describing reality—it is the very language through which matter organizes itself into form. Every crystal serves as a testament to the inherent geometry of existence, where microscopic mathematical relationships manifest into visible beauty through the precise orchestration of atomic and molecular forces. These geometric growth patterns remind us that beneath the apparent chaos of nature lies an exquisite mathematical order, forever expressing itself through the sacred geometry of crystalline form.




